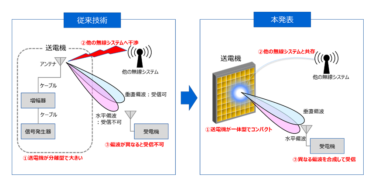
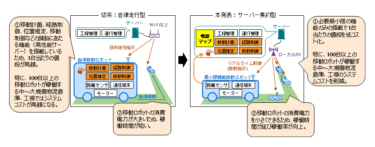
作ったものが人によって違うか否か、原料を変えたことによって製品性能に違いがあるか、製造条件を変更したことによる品質への影響は無いか。
製造業における技術者はしばしば、「変更前後で違いは無いか」ということを判断することが求められます。このような同等性判断をどうするのか、ということの振る舞いによってその技術者の力量が良く見えます。
感覚論が優位になる危機的傾向
同等性判断を求められる局面で、技術者の技術力が低下してきたと実感する瞬間はいくつかありますが、最も大きいのは「同等か否かを感覚論で判断しようとする」という話し合いや技術報告書を読んだ時です。
場合によっては声の大きい担当者の鶴の一声で方向性が決まることもあり、「立場や職場空気」という「技術とは全く無関係な不可解なパラメータ」で技術的な判断をするという、私から見ると全く理解できないことがいくつもあります。
また技術力のある程度高い、もしくは高いと自負している企業では、研究論文や専門書を参考に議論を展開することもあります。仮説を立て、技術的論の裏付けをするのは大変重要であり、基礎技術力を高めるという観点でも異論はありません。
むしろ、的確な判断をするには好ましいといえます。しかし、「同等性を“判断”する」ということが求めらるところでは、仮説を唱えたとしてもそれだけでは「前進することができない」という根本的な問題に直面することになります。
技術的理論や仮説を踏まえ、結局それが同等なのか否かを「判断する」ということが必要だからです。マネジメントとしても理屈をいくら聞かされたとしても、その同等性を判断するというには情報が不十分である可能性があるため、マネジメントも判断できないという苦しい状況に置かれることになります。
では、技術者が同等性を判断するのに必要なスキルは何でしょうか。
同等性判断に有効な統計学のスキル
結論から言うと統計学が技術者が同等性を判断する際の武器となります。まず条件の異なる2つの母集団の平均値、すなわち2つのグループが同じ平均的な数値を示すか否かを判断したいのであれば、「t検定」が有効です。
具体的にはExcelのような表計算ソフトがあるのであれば、「データ分析」というアドインを使えば検証をすることが可能です。「一対の標本によるt検定」というコマンドを使えば検定を行うことができます。
3つ以上の母集団の平均値に有意差があるか否かを調べたいのであれば、分散分析を使うのが妥当です。こちらも例えばExcelであれば「一元配置分散分析」を使うことで評価することが可能です。
詳細は割愛しますが、一元配置はあくまで一つの変数に対する検定なので、2つの変数による平均値の有意差を見たい場合は二元配置を使います。どちらも「母集団間に平均値の差は無い」という帰無仮説を立て、それが統計学的に妥当か否かを判断します。
一般的にはこの有意水準を5%（α=0.05）に設定し、検定の結果算出されるp値（t検定の場合は片側検定）が0.05より下回れば、上記の帰無仮説は棄却され、つまり平均値には差があるという判断になります。
差があるということは「複数のグループは同等ではなく、有意差があると考えられる」という判断をすることと同じになるのです。
理論はきちんと押さえる
上記の通り統計学は同等性を技術的、つまり客観的に判断するのに有効である一方、課題もあります。まず、技術者はきちんと理論の概要を理解することが求められます。
機械的にできてしまうので、意味も理解せずに検定だけを行うのはあまりにも危険です。いくつか推奨できる専門書はありますが、以下の図書が最も実践的でかつ的確な内容ですので、必要に応じて購入されることをお勧めします。
【新編 統計的方法（日本規格協会）森口 繁一 編】アドインを使わなくとも、Excelだけで計算できる上、必要に応じて電卓でも計算できるというのが、上記の図書を読むとよくわかります。
手計算のものと、アドインで計算した結果が同じになるかを一度見てみる、というくらいの取り組みは技術者であれば不可欠でしょう。また、理論を読むとわかりますがこの手の検定には前提があり、その一つが例えば「各母集団データが正規分布である」ということになります。
この前提に則らないと絶対に検定は意味が無いとは言いませんが、正規分布か否かをきちんと検定し、仮に正規分布でなければ、「正規分布であるという仮定が成立していないという前提で（t検定などの）検定結果を見る必要がある」といえることが技術者に求められます。
尚、正規分布の検定にはいくつか手法がありますが、例えばその一つに Anderson Darling 検定があります。
定量的な同等性判断での留意点
ここでいくつかの留意点も述べておきます。まず一つ目が、「検定結果だけをうのみにしない」ということです。技術者の中には検定の結果が出たらそれがすべてと盲信するケースもあります。
より俯瞰的にみることが必要です。一例を述べます。検定結果というのはあくまで数値上の話です。その前提は、「インプットデータが正確である」ということにあります。正規分布か否かという前提の前の大前提といえます。
同等であると判断したい、またはその逆の個人的、会社的動機故にデータを改ざんしていては、そもそも検定に使っているデータが不適切になるため、検定結果は全くあてにならないということになりかねません。
数値分析はインプットデータの質に大きく左右されるため、複数の人が立会いの下データを取得するというくらいの徹底さが必要かもしれません。二つ目が経験則も無視しない、ということです。
定性的なパラメータの固まりともいえる経験則ですが、このすべてを無視するとそれはそれで過去のノウハウを活かせていないことになります。百戦錬磨の技術者の有する経験は大変貴重なものであり、それをうまく活用するのも技術者として大切な姿勢です。
ただし、当然ながら経験はあくまで主観的な要素も入るため、・経験則も盲信しないこと・経験則が正しいか否かを定量的に検証することという取り組みは技術者として不可欠です。
技術的業務内で同等か否かということを検証するにあたり、技術者は統計学のスキルが武器になります。このようなスキルも実務の中で習得する仕組みを整えることが、これからの技術系企業の成長には不可欠といえます。
ご参考になれば幸いです。
【著者】
吉田 州一郎
（よしだ しゅういちろう）
FRP Consultant 株式会社
代表取締役社長
福井大学非常勤講師
FRP（繊維強化プラスチック）を用いた製品の技術的課題解決、該関連業界への参入を検討、ならびに該業界での事業拡大を検討する企業をサポートする技術コンサルティング企業代表。現在も国内外の研究開発最前線で先導、指示するなど、評論家ではない実践力を重視。複数の海外ジャーナルにFull paperを掲載させた高い専門性に裏付けられた技術サポートには定評がある。
https://engineer-development.jp/
オートメーション新聞は、1976年の発行開始以来、45年超にわたって製造業界で働く人々を応援してきたものづくり業界専門メディアです。工場や製造現場、生産設備におけるFAや自動化、ロボットや制御技術・製品のトピックスを中心に、IoTやスマートファクトリー、製造業DX等に関する情報を発信しています。新聞とPDF電子版は月3回の発行、WEBとTwitterは随時更新しています。
